Rational Numbers Between Two Rational Numbers – Examples, FAQs

What Are Rational Numbers between Two Rational Numbers?

There are infinitely many rational numbers between any two distinct rational numbers.

If you consider any two natural numbers, there will be only a finite number of natural numbers between them. For example, between the natural numbers 8 and 14, there are only five natural numbers, which are 9, 10, 11, 12, and 13.

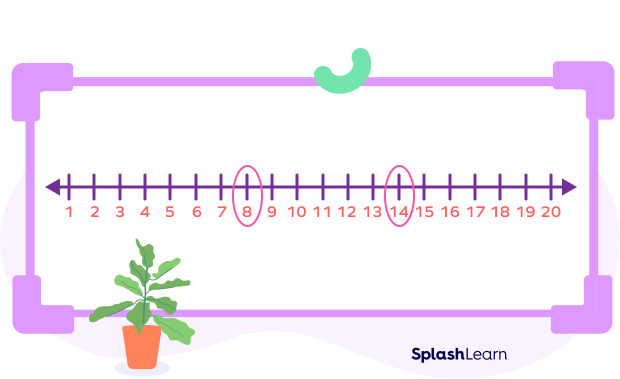
However, that’s not the case with rational numbers.

Rational numbers are numbers that can be written in the form $\frac{p}{q}$, where p and q are integers, and $q \neq 0$. The set of rational numbers include integers, fractions, terminating decimals, and non-terminating repeating decimals. 

If you take any two rational numbers, you can divide the segment on the number line joining these two numbers into infinitely many parts and get infinitely many numbers of the form $\frac{p}{q}$, where p and q are integers, and $q \neq 0$. 

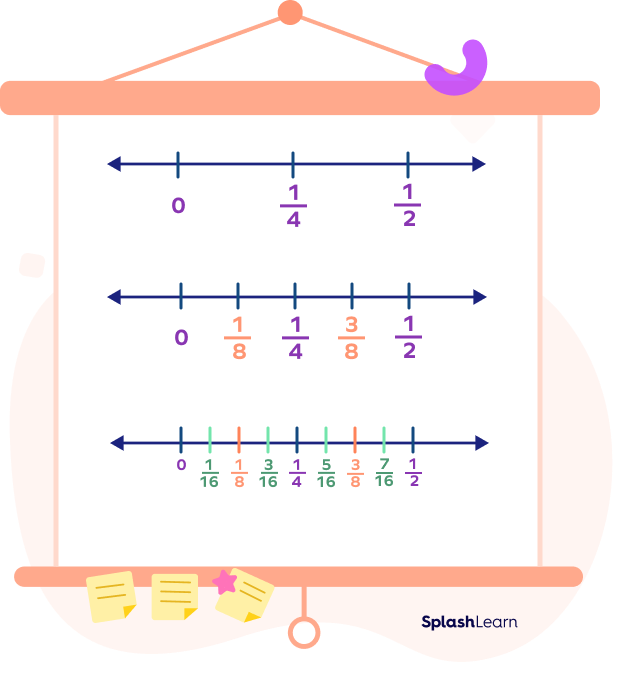
Example: Consider two rational numbers $\frac{1}{4}$ and $\frac{1}{2}$.

Let’s plot them on a number line. Divide the segment joining $\frac{1}{4}$ and $\frac{1}{2}$ into two equal parts, we get $\frac{3}{8}$ as the midpoint. Dividing each small segment, we get more and more such rational numbers. Same goes for the rational numbers between 0 and $\frac{1}{4}$.

Note: 

The difference between rational numbers and fractions lies in the fact that fractions cannot have negative numerator or denominator. Hence, the numerator and denominator of a fraction are whole numbers (denominator ≠ 0), whereas in the case of rational numbers, the numerator and denominator are integers (denominator ≠ 0).

How to Find Rational Numbers between Two Rational Numbers

We can find the rational numbers between any two rational numbers using simple methods.

We will discuss two cases.

Case 1: Given rational numbers have the same denominator

Case 1: Given rational numbers have the different denominators

Rational Numbers between Two Rational Numbers with the Same Denominator

If the two rational numbers have the same denominator, identifying a few rational numbers between them is simple.

Step 1: Check the value of the numerators. Write all the natural numbers between these two numbers. 

Step 2: Write all the rational numbers with these natural numbers as numerators and keep the same denominator. Write these rational numbers in the increasing order of the numerators for better understanding.

Example: Find the rational numbers between $\frac{3}{5}$ and $\frac{9}{5}$. 

Denominator of both rational numbers is the same, 5.

Numerators are 3 and 9.

Natural numbers between them are 4, 5, 6, 7, and 8.

We can write find five rational numbers between $\frac{3}{5}$ and $\frac{9}{5}$ by choosing 4, 5, 6, 7, and 8 as numerators and keeping 5 as the denominator.

Five rational numbers between $\frac{3}{5}$ and $\frac{9}{5}$ are $\frac{4}{5}, \frac{5}{5}, \frac{6}{5}, \frac{7}{5}$, and $\frac{8}{5}$. 

What if we are asked to find more rational numbers between $\frac{3}{5}$ and $\frac{9}{5}$? 

Let’s understand how we can do that.

If we multiply and divide both the numbers by 10 (or , we will get their equivalent rational numbers. Equivalent rational numbers are the rational numbers that, when reduced to the simplest form, have the same value. They are located at the same point on the number line. 

Here, we get 

$\frac{3 \times 10}{5 \times 10} = \frac{30}{50}$ and $\frac{9 \times 10}{5 \times 10} = \frac{90}{50}$

Note that $\frac{3}{5} = \frac{30}{50}$ and $\frac{9}{5} = \frac{90}{50}$.

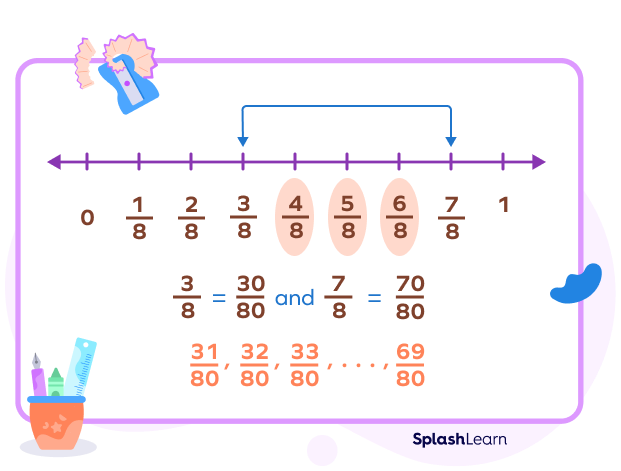
Now, we can easily write ten rational numbers between $\frac{30}{50}$ and $\frac{90}{50}$, such as

 $\frac{31}{50}, \frac{32}{50}, \frac{37}{50}, \frac{39}{50}, \frac{45}{50}, \frac{67}{50}, \frac{68}{50}, \frac{78}{50}, \frac{84}{50}, \frac{88}{50}$.

We can go further and write them in their simplest form, if required.

For example, $\frac{45}{50} = \frac{9}{10}$

(Do not forget that there are infinite rational numbers between two given rational numbers. We are only trying to list a few of them.)

Rational Numbers between two Rational Numbers with Different Denominators

When we have to find the rational numbers between two rational numbers with different denominators, we first make the denominators equal using the LCM method. 

Once the denominators are equal, we can use the method we discussed earlier.

Example 1: Find five rational numbers between $\frac{1}{3}$ and $\frac{2}{7}$.

LCM(3, 7) = 21

$\frac{1 \times 7}{3 \times 7} = \frac{7}{21}$ 

$\frac{2 \times 3}{7 \times 3} = \frac{6}{21}$

Now, since the difference between the numerators is too less, let’s find their equivalent rational numbers.

Multiplying the numerator and denominator by 10, we get

$\frac{6 \times 10}{21 \times 10} = \frac{60}{210}$ and

$\frac{7 \times 10}{21 \times 10} = \frac{70}{210}$

Five rational numbers between $\frac{1}{3}$ and $\frac{2}{7}$ are $\frac{61}{120}, \frac{65}{120}, \frac{66}{120}, \frac{67}{120}, \frac{69}{120}$. 

Example 2: Find three rational numbers between $\frac{-3}{5}$ and $\frac{-1}{3}$.

Let’s make the denominators equal.

LCM(3, 5) = 15

$\frac{-3 \times 3}{5 \times 3} = \frac{-9}{15}$ 

$\frac{-1 \times 5}{3 \times 5} = \frac{-5}{15}$ 

Thus, $\frac{-3}{5} = \frac{-9}{15}$ and $\frac{-1}{3} = \frac{-5}{15}$.

We can write

$\frac{-9}{15} \lt \frac{-8}{15} \lt \frac{-7}{15} \lt \frac{-6}{15} \lt \frac{-5}{15}$

 Thus, 

$\frac{-3}{5}\lt \frac{-8}{15} \lt \frac{-7}{15} \lt \frac{-6}{15} \lt \frac{-1}{3}$

Arithmetic Mean Method to Find Rational Numbers between Two Rational Numbers

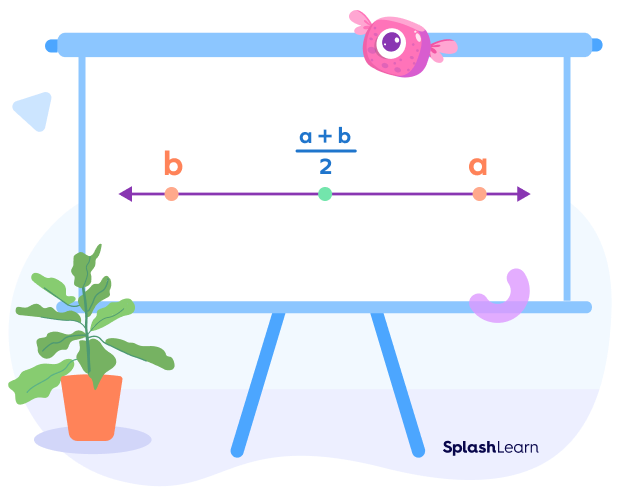
We know that the mean or average of two values is the central value. So, if we find the arithmetic mean of any two rational numbers, we will get a rational number that lies between them. 

Note that it doesn’t matter if the denominators are same or different when we use this method. It is applicable to any two rational numbers.

Example: Find three rational numbers between $\frac{1}{3}$ and $\frac{2}{7}$.

Rational number between $\frac{1}{3}$ and $\frac{2}{7} = \frac{1}{2}(\frac{1}{3} + \frac{2}{7}) = \frac{1}{2}(\frac{7 + 6}{21}) = \frac{13}{42}$

Finding the Next Rational Numbers:

Rational number between $\frac{1}{3}$ and $\frac{13}{42} = \frac{1}{2}(\frac{1}{3} + \frac{13}{42}) = \frac{1}{2}(\frac{1}{4} + \frac{13}{42}) = \frac{27}{84}$

Rational number between $\frac{2}{7}$ and $\frac{13}{42} = \frac{1}{2}(\frac{2}{7} + \frac{13}{42}) = \frac{1}{2}(\frac{12 + 13}{42}) = \frac{25}{84}$

Facts about Rational Numbers Between Two Rational Numbers

Conclusion

In this article, we learned how to find rational numbers between two rational numbers with the help of two cases: i) finding rational numbers between two rational numbers with same denominators, and ii) finding rational numbers between two rational numbers with different denominators. Let’s solve a few examples and practice MCQs to revise and practice!

Solved Examples on Rational Numbers between Two Rational Numbers

1. Find two rational numbers between $\frac{1}{7}$ and $\frac{4}{7}$.

Solution: 

The denominator of $\frac{1}{7}$ and $\frac{4}{7}$ is the same, 7. 

The rational numbers between $\frac{1}{7}$ and $\frac{4}{7}$ are $\frac{2}{7}$ and $\frac{3}{7}$. 

2. What are the three rational numbers between 2 and 3?

Solution: 

Rational number between 2 and 3 $= \frac{1}{2}(2 + 3) = \frac{5}{2}$

Rational number between 2 and $\frac{5}{2} = \frac{1}{2}(2 + \frac{5}{2}) = \frac{1}{2} \times \frac{9}{2} = \frac{9}{4}$

Rational number between 3 and $\frac{5}{2} = \frac{1}{2}(3 + \frac{5}{2}) = \frac{1}{2} \times \frac{11}{2} = \frac{11}{4}$

3. Find four rational numbers between $\frac{2}{5}$ and $\frac{3}{8}$.

Solution: 

Denominators are different.

LCM of 5 and 8 = 40

$\frac{2 \times 8}{5 \times 8} = \frac{16}{40}$ and $\frac{3 \times 5}{8 \times 5} = \frac{15}{40}$

$\frac{16 \times 10}{40 \times 10} = \frac{160}{400}$ and $\frac{15 \times 10}{40 \times 10} = \frac{150}{400}$

Four rational numbers between $\frac{2}{5}$ and $\frac{3}{8}$ are $\frac{162}{400}, \frac{164}{400}, \frac{167}{400}$, and $\frac{169}{400}$. 

In simplest form, we can write them as $\frac{81}{20}, \frac{41}{10}, \frac{167}{400}$ and $\frac{169}{400}$

4. Determine one rational numbers between $\frac{9}{11}$ and $\frac{12}{13}$.

Solution:

The arithmetic mean to rational numbers is a rational number that lies between them.

Rational number between $\frac{9}{11}$ and $\frac{12}{13} = \frac{1}{2}(\frac{9}{11} + \frac{12}{13})$

$= \frac{1}{2}(\frac{(13 \times 9) + (11 \times 12)}{11 \times 13})$

$= \frac{1}{2}(\frac{117 + 132}{143})$

$= \frac{249}{286}$

5. Determine six rational numbers between $\frac{1}{2}$ and $\frac{2}{3}$.

Solution:

$\frac{1 \times 3}{2 \times 3} = \frac{3}{6}$ and $\frac{2 \times 2}{3 \times 2} = \frac{4}{6}$

$\frac{3 \times 10}{6 \times 10} = \frac{30}{60}$ and $\frac{4 \times 10}{6 \times 10} = \frac{40}{60}$

Six rational numbers between $\frac{1}{2}$ and $\frac{2}{3}$ are $\frac{31}{60}, \frac{33}{60}, \frac{34}{60}, \frac{35}{60}, \frac{37}{60}$, and $\frac{39}{60}$.

Practice Problems on Rational Numbers between Two Rational Numbers

Frequently Asked Questions about Rational Numbers between Two Rational Numbers