- What Is the Fundamental Theorem of Arithmetic?
- Fundamental Theorem of Arithmetic Statement
- Why Is the Fundamental Theorem of Arithmetic Important?
- Solved Examples on Fundamental Theorem of Arithmetic
- Practice Problems on Fundamental Theorem of Arithmetic
- Frequently Asked Questions about the Fundamental Theorem of Arithmetic
What Is the Fundamental Theorem of Arithmetic?
The fundamental theorem of arithmetic is also known as the unique factorization theorem or the unique-prime-factorization theorem.
According to the fundamental theorem of arithmetic, every integer greater than 1 is either a prime number or it can be expressed as the unique product of its prime factors (ignoring the order of the prime factors).
This theorem further states that the factorization of each composite number is unique
(order in which prime factors are written is not taken into account).
Any integer greater n than 1 can be written as the product of its prime factors as
$n = p_{1} \times p_{2} \times $….$p_{n}$, where $p_{1},\;p_{2}$,….,$p_{n}$ are prime factors (not distinct because we have not mentioned the exponents) written in ascending order such that $p_{1} \le p_{2}\le$….$\le p_{n}$. The ascending order ensures that the factorization is unique.
Prime numbers are numbers greater than 1 that have only two factors, 1 and the number itself. Examples: 2, 3, 5, 7, 11, 13, 17, 19, …
Suppose we have to find the prime factorization of 360.
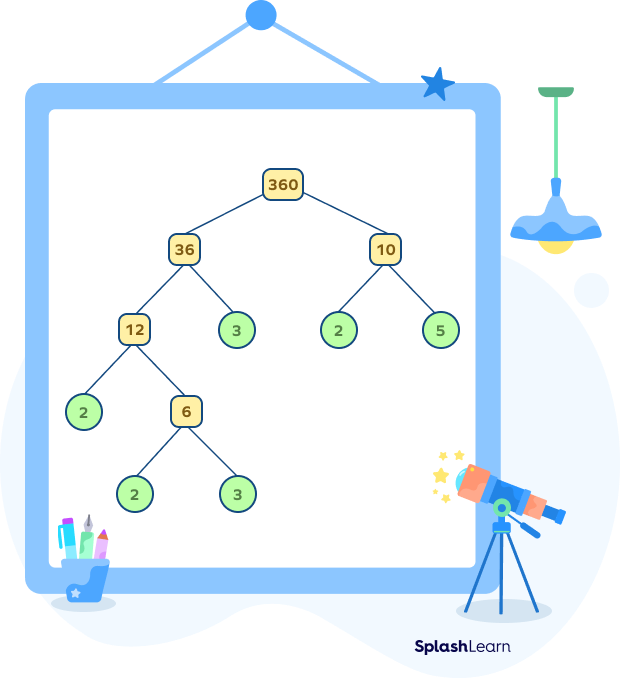
Using the factor tree of 360, we can write
$360 = 2 × 2 × 2 × 3 × 3 × 5$
$360 = 3^{2} × 2^{3} × 5^{1}$
It means that there is no other way to express 360 as a product of primes. We can obviously change the order in which the prime factors occur, but $360 = 3^{2} × 2^{3} × 5^{1}$ is the unique factorization of 360.
Here are a few more examples.
| 2 | Prime Number |
| 3 | Prime Number |
| 4 | $4 = 2 × 2 = 2^{2}$ |
| 5 | Prime Number |
| 6 | $6 = 2 × 3$ |
| 7 | Prime Number |
| 8 | $8 = 2 × 2 × 2 = 2^{3}$ |
| 9 | $9 = 3 × 3 = 3^{2}$ |
| 10 | $10 = 2 × 5$ |
| 11 | Prime Number |
| 12 | $12 = 2 × 2 × 3 = 2^{2} × 3$ |
| 13 | Prime Number |
| 14 | $14 = 2 × 7$ |
| 15 | $15 = 3 × 5$ |
Fundamental Theorem of Arithmetic Statement
Every integer greater than 1 is either a prime number, or can be expressed uniquely as a product of prime numbers (the factorization is unique except for the order).
Fundamental Theorem of Arithmetic Proof
To prove the fundamental theorem of arithmetic, we need to prove the existence and the uniqueness of the prime factorization.
To prove: Every integer greater than 1 can be uniquely expressed as a product of primes.
Step 1: Existence of Prime Factorization
We will prove this using mathematical induction.
The statement is true for $n = 2$ since 2 is a prime number.
Let us assume that the statement is true for all n such that $1\lt n \lt k$.
It means that we can write every n where $1\lt n \lt k$ as the product of primes. …(1)
Let us prove that the statement is true for $n = k$.
If k is prime, then the case is obvious.
If k is not prime, then it is a composite number and we can factor it as
$k = x \times y$ where $1\lt x,\;y \lt k$ …(2)
From (1) and (2), we can say that x and y can be written as the product of primes.
Thus, k can also be written as the product of primes.
Thus, by mathematical induction, the “existence of factorization” is proved.
Step 2: Uniqueness of Prime Factorization
Now, let us suppose that n can be written as the product of primes in two different ways, say,
$n = p_{1}^{m_{1}} \times p_{2}^{m_{2}} \times $….$\times p_{i}^{m_{n}}$
$n = q_{1}^{n_{1}} \times q_{2}^{n_{2}} \times $….$\times q_{j}^{n_{j}}$
Thus, $n = p_{1}^{m_{1}} \times p_{2}^{m_{2}} \times $….$ \times p_{i}^{m_{n}} = q_{1}^{n_{1}} \times q_{2}^{n_{2}}\times$….$\times q_{j}^{n_{j}}$ …(1)
where, the p’s and the q’s are distinct primes.
Euclid’s lemma: If $p| ab$, then $p|a$ or $p|b$.
Here, $p_{1}$ divides the expression on the left side. So, it also divides the expression on the right side.
Thus, $p_{1}$ divides $q_{1}^{n_{1}} \times q_{2}^{n_{2}}\times$…. $\times q_{j}^{n_{j}}$.
By Euclid’s lemma, $p_{1}$ divides $q_{k}^{n_{k}}$ for some k.
Here, $q_{k}^{n_{k}} = q_{k} \times q_{k}\times$ ….$\times q_{k}\;(n_{k} \text{times})$
Again by the same lemma, $p_{1}$ divides $q_{k}$.
However, both $p_{1}$ and $q_{k}$ are primes.
So, $p_{1} = q_{k}$
For convenience and to avoid confusion, let $p_{1} = q_{1}$ (our choice of k was random)
We can write (1) as
$n = p_{1}^{m_{1}} \times p_{2}^{m_{2}}\times$….$\times p_{i}^{m_{n}} = p_{1}^{n_{1}} \times q_{2}^{n_{2}}\times$….$\times q_{j}^{n_{j}}$
This is true if and only if $m_{1} = n_{1}$.
If $m_{1} \gt n_{1}$, we can cancel out the term p1n1 from the right side. It will not make sense that p1divides only the LHS and not the RHS.
Thus, $m_{1} = n_{1}$
Canceling out the p1 terms on both sides, we get
$n = p_{2}^{m_{2}}\times$….$\times p_{i}^{m_{n}} = q_{2}^{n_{2}}\times$….$\times q_{j}^{n_{j}}$
Following the same steps, we can pair up p’s and the q’s and conclude that the factorization is unique (except possibly for the order).
HCF and LCM Using Fundamental Theorem of Arithmetic
We use the fundamental theorem of arithmetic for finding the HCF and LCM of two or more numbers.
- GCF is the product of the smallest power of each common prime factor. It is also known as the GCD (Greatest Common Divisor) or GCF(Greatest Common Factor).
- LCM is the product of the greatest power of each prime factor.
Example: Find the GCF of 120 and 180.
Prime factorization of $120 = 2^{3} × 3^{1} × 5^{1}$
Prime factorization of $180 = 2^{2} × 3^{2} × 5^{1}$
Since, HCF can be defined as the product of the smallest power of each common prime factor.
Common factors $= 2, 3, 5$
Smallest powers of 2, 3, and 5 are 22, 31, and 51 respectively.
Hence, HCF (120, 180) $= 2^{2} × 3^{1} × 5^{1} = 60$.
Since LCM can be defined as the product of the greatest power of each prime factor. Hence, LCM (120, 180) $= 2^{3} × 3^{2} × 5^{1} = 360$.
Why Is the Fundamental Theorem of Arithmetic Important?
The theorem plays a crucial role in number theory and provides a fundamental understanding of the properties and relationships of numbers.
- The theorem forms the foundation for many number theory concepts and allows us to solve a wide range of mathematical problems.
- It allows us to break down any number into its prime factors using Prime Factorization, providing valuable information about its properties and structure.
- By decomposing a number into its prime factors, we can easily determine if it is divisible by another number and identify its factors.
- The theorem guarantees that the prime factorization of a number is unique. This means that two different numbers cannot have the same prime factorization
Facts about Fundamental Theorem of Arithmetic
- Prime numbers are considered as the basic building blocks of all numbers.
- The fundamental theorem of arithmetic is important because it tells you what each number is composed of. It helps you understand how each number is made of prime factors.
- Euclid’s Lemma: Let p be a prime, and let a, b be integers. If p | ab then p | a or p | b.
Conclusion
In this article, we learned about the fundamental theorem of arithmetic, its statement and proof along with its applications in finding the LCM and HCF. Let’s move ahead and solve some examples based on these concepts.
Solved Examples on Fundamental Theorem of Arithmetic
1. Express 198 as the product of prime factors.
Solution:
By using the fundamental theorem of arithmetic, we know that we can express 198 as a product of its prime factors. We will find the prime factorization of 198.
Prime factorization of 198:
$198 = 2 × 99$
$198 = 2 × 3 × 33$
$198 = 2 × 3 × 3 × 11$
$198 = 2^{1} × 3^{2} × 11^{1}$
2. How can you express 1075 as the product of prime factors using the fundamental theorem of arithmetic?
Solution:
By using the fundamental theorem of arithmetic, we know that we can express 1075 as a product of its prime factors. We will find the prime factorization of 1075.
Prime factorization of 1075:
$1075 = 5 × 5 × 43$
$1075 = 5^{2} × 43^{1}$
3. Find the GCF of 140, 210 and 350 using the fundamental theorem of arithmetic.
Solution:
Prime factorization of $140 = 2 × 2 × 5 × 7 = 2^{2} × 5^{1} × 7^{1}$
Prime factorization of $210 = 2 × 3 × 5 × 7 = 2^{1} × 3^{1} × 5^{1} × 7^{1}$
Prime factorization of $350 = 2 × 5 × 5 × 7 = 2^{1} × 5^{2} × 7^{1}$
GCF(140, 210 and 350) $=$ Product of the smallest power of each common prime factor
GCF(140, 210 and 350) $= 2^{1} × 5^{1} × 7^{1} = 70$
4. Using the fundamental theorem of arithmetic, find the LCM of 50, 75 and 105.
Solution:
Prime factorization of $50 = 2 × 5 × 5 = 2^{1} × 5^{2}$
Prime factorization of $75 = 3 × 5 × 5 = 3^{1} × 5^{2}$
Prime factorization of $105 = 3 × 5 × 7 = 3^{1} × 5^{1} × 7^{1}$
LCM(50, 75 and 105) $=$ Product of the greatest power of each prime factor
LCM(50, 75 and 105) $= 2^{1} × 3^{1} × 5^{2} × 7^{1} = 1050$
Practice Problems on Fundamental Theorem of Arithmetic
Fundamental Theorem of Arithmetic - Definition, Proof, Examples, FAQs
Which of the following is the correct prime factorization for 756?
The prime factorization of $756 = 2 \times 2 \times 3 \times 3 \times 3 \times 7 = 2^{2} \times 3^{3} \times 7^{1}$
Which of the following is the prime factorization of 1575?
$1575 = 3 \times 3 \times 5 \times 5 \times 7 = 3^{2} \times 5^{2} \times 7^{1}$
Which of the following is the LCM of $2^{3} \times 5^{2} \times 7^{1}$ and $2^{2} \times 5^{3} \times 7^{2}$?
LCM is the product of the greatest power of each common prime factor.
So, LCM $(2^{3} \times 5^{2} \times 7^{1},\; 2^{2} \times 5^{3} \times 7^{2}) = 2^{3} \times 5^{3} \times 7^{2}$
By the fundamental theorem of arithmetic, every integer greater than 1 is either a/an ______ or can be expressed uniquely as the product of prime factors.
Any integer greater than 1 is either a prime number, or can be expressed uniquely as a product of prime numbers (the factorization is unique except for the order).
Which of the following is the smallest prime number?
The smallest prime number is 2.
Frequently Asked Questions about the Fundamental Theorem of Arithmetic
Why is the fundamental theorem of arithmetic important? Why is it called the fundamental theorem of arithmetic?
The theorem is important as it ensures the existence and the uniqueness of the prime factorization of a number. It has applications in finding the HCF and LCM. It is termed as “fundamental” because it gives you an important insight into the structure of numbers or how numbers are made of prime numbers. It establishes the fact that the prime numbers are the building blocks of the numbers.
Who made notable contributions to the fundamental theorem of arithmetic?
Both Euclid and Gauss made notable contributions to the understanding and proof of the theorem. Euclid provided an informal statement of the theorem in his work “Elements.” However, it was Carl Friedrich Gauss who first proved the theorem formally in 1801. Another name in this list is the Greek mathematician Diophantus.
Are 0 and 1 prime numbers?
0 and 1 are neither prime nor composite.
What are fundamental rules of arithmetic?
The fundamental rules of arithmetic refer to the order of operations, addition and subtraction involving negative numbers, multiplication and division involving negative numbers. These rules are important in evaluating expressions.
















