What Is a Square Prism?
A square prism is a special type of a cuboid (a rectangular prism) in which the bases are squares.
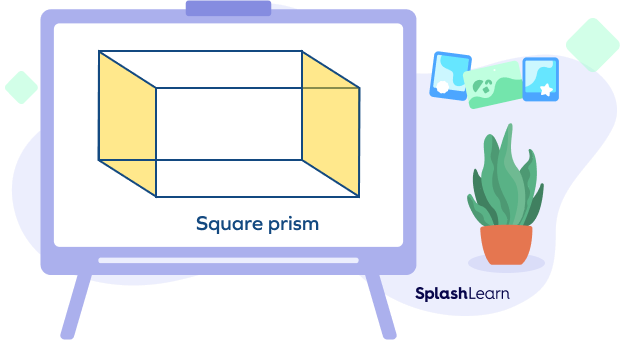
A prism is a polyhedron or a solid shape that is formed with flat faces. The top and bottom faces are identical and are called bases. A prism is named after the shape of these bases.
For example, if a prism has a triangular base, it is called a triangular prism. If the base is a rectangle, it is called a rectangular prism. So, in a square prism, the base is a square.
Recommended Games
Square Prism: Definition
A square prism is a three-dimensional shape whose bases are squares and the four lateral faces are rectangular in shape.
Opposite faces of a square prism are congruent.
Recommended Worksheets
Properties of Square Prism
- A square prism has 6 faces, 12 edges, and 8 vertices.
- Opposite sides of a square prism are parallel and congruent to each other.
- Opposite angles of a square prism are congruent to each other.
- Diagonals of a square prism bisect each other.
- Consecutive angles of square prisms are supplementary.
(Note: A face or a flat surface of a solid is also called its side. So, here, “side” of a square prism refers to its faces.)
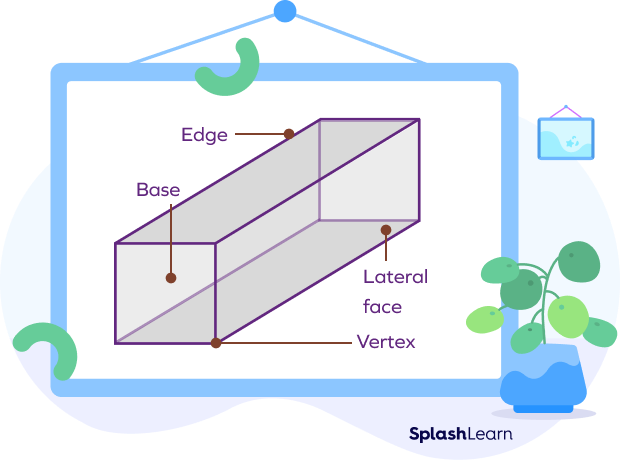
Types of a Square Prism
Square prisms are of two types based on the position of the lateral faces with respect to the base.
- Right Square Prism
- Oblique Square Prism
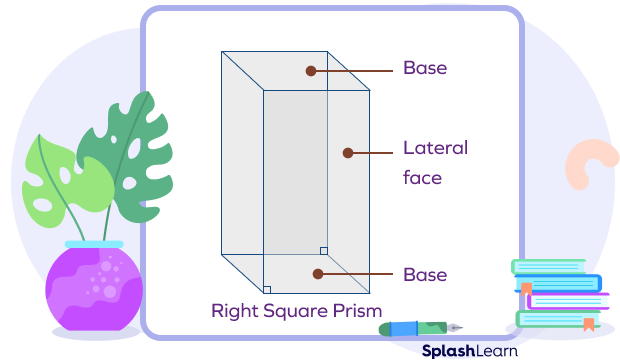
Right Square Prism
In a right square prism, the lateral faces (the rectangular faces) are perpendicular to its bases. This means that the two bases line up or get aligned with one directly above the other.
Oblique Square Prism
In an oblique square prism, the rectangular faces are not perpendicular to the prism’s bases. Although the two bases will be congruent and parallel, one is not placed directly over the other.

Surface Area of a Square Prism
The surface area (or total surface area) of a square prism is the total area of all its faces (two square bases and four rectangular lateral faces).
It can be defined as the sum of the lateral surface area and the area of two square bases.
Surface area of a prism is measured in square units such as $ft^{2},\; in^{2}$, etc.
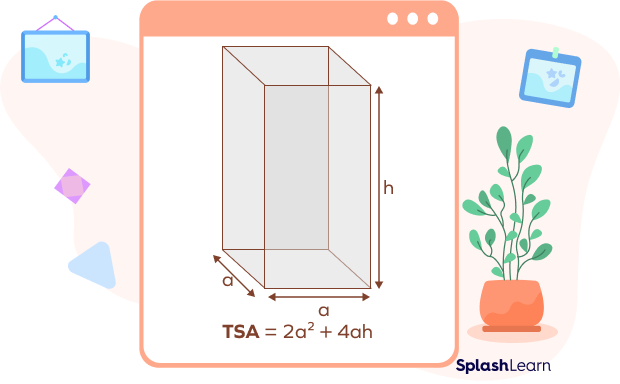
In the image above, we have a square prism where
“a” is the side length of the square at the base
“h” is the height of the square prism.
Lateral surface area of a square prism $=$ Area of 4 rectangular faces
LSA $= 4(ah)$
Area of the base $= a^{2}$
The formula for the surface area of the square prism is given by
Total surface area of the square prism $= (2 \times \text{Base area}) + \text{Lateral surface area}$
$TSA = 2a^{2} + 4ah$ square units.
Volume of a Square Prism
Every 3D shape occupies some space. This space is measured in terms of its volume. Volume is defined as the space occupied within the boundaries of an object in three-dimensional space.
Volume is measured in cubic units such as $ft^{3},\; inch^{3}$, etc.
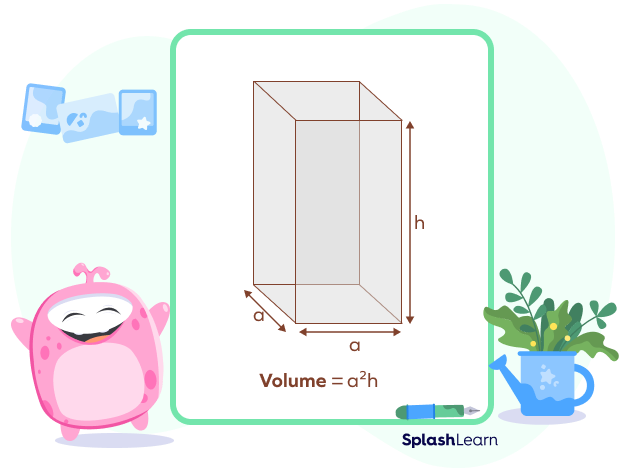
Volume of a square prism is given by the product of the base area and its height.
$\text{Volume of a Square Prism} = \text{Base area}$
$\text{Base area} = \text{Area of a square with side “a”} = a^{2}$
Height $=$ h
Volume of a Square Prism $= V = a^{2}h$ cubic units.
where,
“a” is the base-edge (side of the square at the base).
“h” is the height of the square prism.
Square Prism Formulas
Let a be the base-edge of the square prism (side-length of the square at the base) and h be the height of the square prism.
- Lateral Surface Area of a Square Prism $= 4ah$
- Total Surface Area of a Square Prism $= 2a^{2} + 4ah$
- Volume of a Square Prism $= a^{2}h$
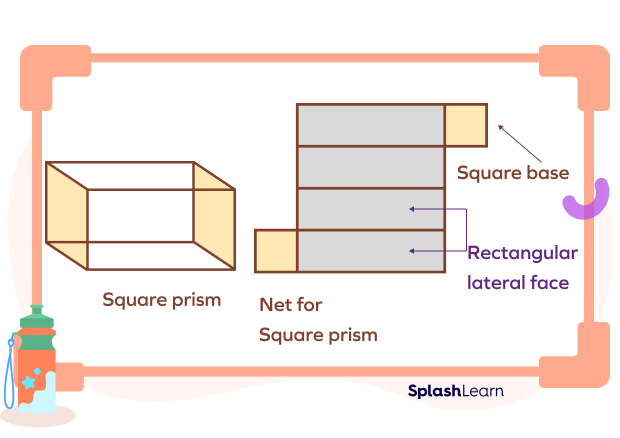
Square Prism Net
When the square prism is flattened by opening it along the edges, the 2D structure formed as a result is known as the net of the square prism. It has 2 square faces and 4 rectangular faces.
When all flattened ends are joined back, we get the shape of a square prism. The image below shows the net of the square prism.
Facts about Square Prism
- A square prism is a cuboid (a convex polyhedron), which has 6 faces, out of which two end-faces are square, 4 lateral faces are rectangles.
- It has 12 edges, out of which 4 are lateral edges and 8 edges are of end faces.
- It has 8 vertices (4 vertices of the square face at the top and 4 vertices of the other square at the base).
- All square prisms are not cubes, but all cubes are square prisms. This is because every cube fulfills the properties of a square prism.
- As a Rubik’s cube has six congruent faces that are all perpendicular to each other, a Rubik’s cube is a well-known example of a square prism.
Conclusion
In this article, we have learned about the definition, types, properties, and formulas of the square prism. Let’s solve some examples based on those formulas to understand the concept better.
Solved Examples on a Square Prism
1: Find the total surface area of the given square prism.
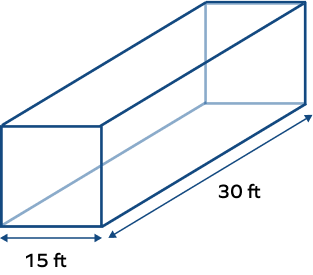
Solution:
Height of the square prism $(h) = 30$ ft
The side length of the square in square prism $(a) = 15$ ft
Base area of a square prism $= a^{2}$
The lateral surface area of square prism $= 4ah$
where “a” is the side length of the base square and “h” is the height of the square prism
Total surface area of the given square prism $= (2\times \text{Base area}) + \text{Lateral surface area}$
$= (2 \times 15^{2}) + (4 \times 15 \times 30)$
$= (2 \times 225) + 1800$
$= 450 + 1800$
$= 2250$ square ft
Total surface area of the given square prism $= 2250$ square feet.
2. Find the volume of a square prism if the length of the side of the square face of a square prism is 10 in and height is 12 in.
Solution:
Height of the square prism $(h) = 12$ in
The side length of the square in square prism $(a) = 10$ in
Volume of a Square Prism is calculated using the formula:
$V = a^{2}h$ cubic units.
$V = 10^{2} \times 12$
$= 100 \times 12$
$= 1200\; in^{3}$
Volume of the given square prism is $1200\; in^{3}$.
3. Find the side length of the square prism if the volume of the square prism is 1078 cu. units and the height is 22 units.
Solution:
The height of a square prism $(h) = 22$ units
The volume of a square prism $= 1694$ cu. cm
We have,
The Volume of a square prism $= a^{2}h$ cubic units.
By substituting the values in the formula, we get
$1078 = (a^{2}) \times (22)$
$a^{2} = 1078 \div 22$
$a^{2} = 49$
$a = \sqrt{49}$
$a = 7$ units
The side length of the square prism is 7 units.
4. Find the height of the square prism shaped box if the side length of the base is 10 ft and volume is 1500 $ft^{3}$.
Solution:
Volume of the box $= 1500\; ft^{3}$
Side of the base$ = 10\; ft$
Volume of a square prism $= a^{2}h$ cubic units.
By substituting the values in the formula, we get
$1500 = (10^{2}) \times h$
$1500 = 100 \times h$
$h = \frac{1500}{100}$
$h = 15$ ft.
The height of the square prism shaped box is 15 ft.
Practice Problems on a Square Prism
Square Prism - Definition, Types, Properties, Formulas, Facts, FAQs
A square prism is a special case of a ________.
A square prism is a special case of a cuboid where the two bases are squares.
A square prism has
A square prism has 6 faces out of which two bases (top and bottom) are square, 4 lateral faces are rectangles.
Volume of a square prism is calculated using the formula: $V =$ ________.
Volume of a Square Prism is calculated using the formula: $V = \text{Base area}\times \text{height}$
$V = a^{2}h$ cubic units.
where,
“a” is the side length of the square prism
“h” is the height of the square prism.
Total surface area of the square prism (TSA) is given by
The surface area can be defined as the sum of the lateral surface area (LSA) and the area of the 2 square bases of the prism. It is calculated using the formula $TSA = 2a^{2} + 4ah$ square units.
Frequently Asked Questions on Square Prism
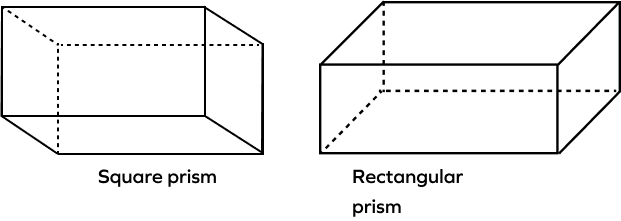
What is the difference between a square prism and a rectangular prism?
A rectangular prism has six faces, and all the faces are rectangles. A square prism has two square bases and four rectangular lateral faces.
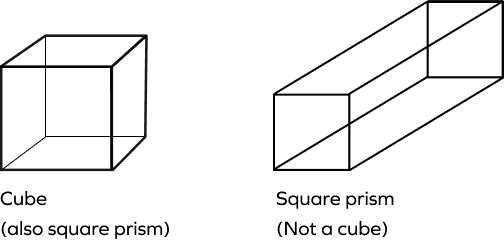
Are cube and square prisms the same? Is a square prism always a cube?
A cube is a 3D shape in which all edges have the same length. A square prism is a cuboid with a square base. However, it is not necessary that the height will be the same as the side of the square. Thus, every square prism is not a cube. So, a square prism becomes a cube when all the edges are equal in length. Every cube is a square prism as it satisfies the properties of a square prism.
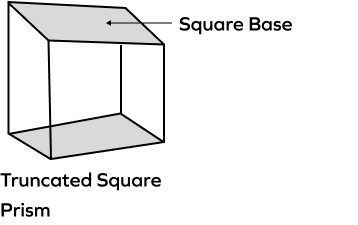
What is a truncated square prism?
A truncated square prism is a portion of a prism formed by the intersection of a plane not parallel to the base such that the plane is intersecting all the lateral edges. Since the truncating plane is not parallel to the base, the solid formed has two nonparallel bases, which are both polygons of the same number of edges. In a truncated square prism, the lateral edges are non-congruent and the lateral faces are quadrilaterals.
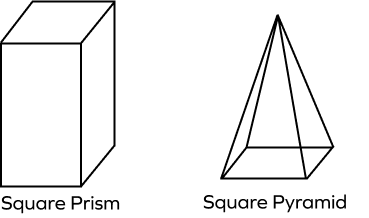
What is the difference between a square pyramid and a square prism?
Both the square pyramid and square prism have a square base, but the four lateral faces of a square pyramid are triangular in shape, which join together at the apex, whereas the four lateral faces of a square prism are rectangular in shape such that the top and base are parallel and congruent.