- What Is the Difference between Square and Rectangle?
- What Are the Properties of Squares and Rectangles?
- Difference between a Square and a Rectangle
- Solved Examples on the Difference between Square and Rectangle
- Practice Problems on Difference between Square and Rectangle
- Frequently Asked Questions on the Difference between Square and Rectangle
What Is the Difference between Square and Rectangle?
Squares and rectangles are quadrilaterals. The major difference between square and rectangle is, all sides of a square are equal, on the other hand, only opposite sides of a rectangle are equal.
Take a look at the shape of a square and a rectangle to get a better idea!
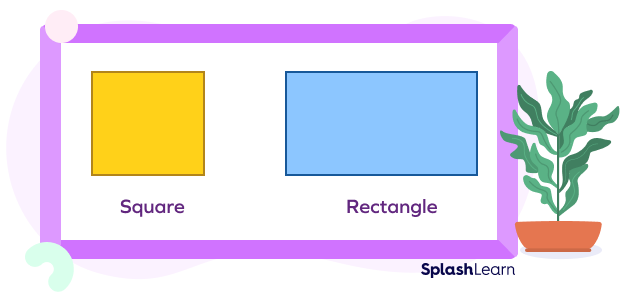
Recommended Games
Definition of Square and Rectangle
A square and a rectangle are both quadrilaterals (or polygons with 4 sides). Let’s understand the definitions.
Definition of Square
A square is a quadrilateral with four equal sides, four vertices, and four interior angles measuring 90°.
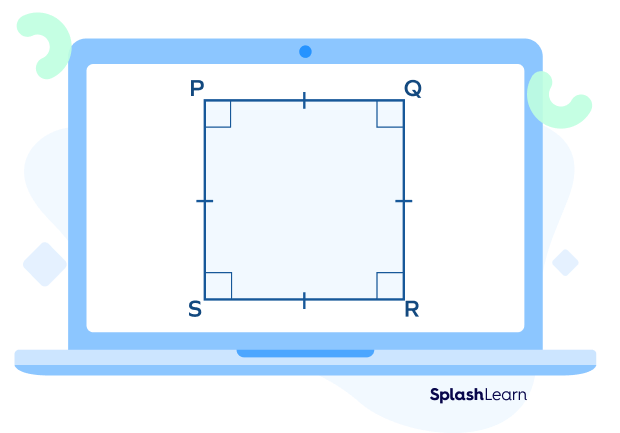
A square is a regular polygon since all its sides are equal and all angles are congruent.
A chessboard is the best example of a square shape in daily life. Observe that there are also 64 small squares on a chess board.

Rectangle
A rectangle is a quadrilateral in which the opposite sides are parallel and equal to each other and all four angles measure $90^{\circ}$.
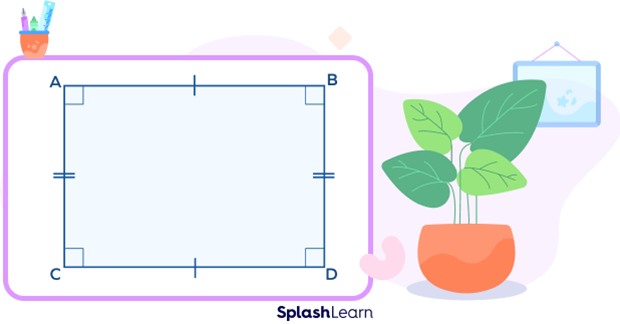
The longer side of a rectangle is called length. The shorter side is called breadth.
Some examples of rectangles around us are dollar bills, chalkboard, books, etc.

Recommended Worksheets
What Are the Properties of Squares and Rectangles?
Let’s learn some of the important characteristics of a square and a rectangle. It will help us in identifying the important differences between them.
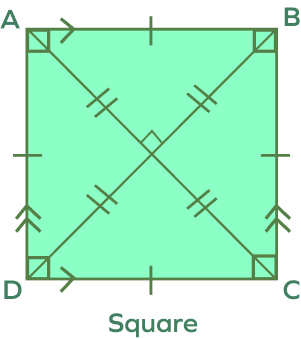
Properties of a Square
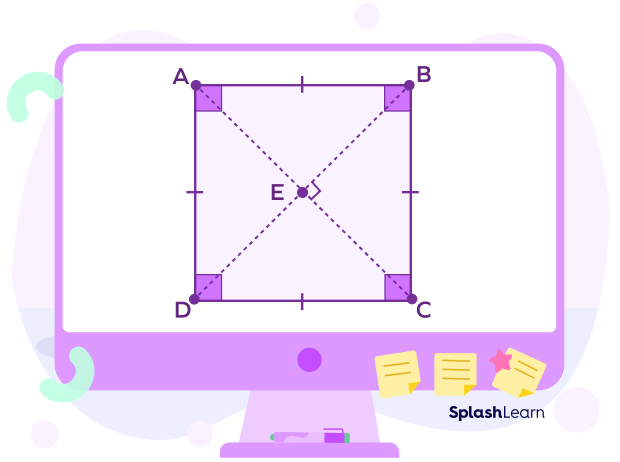
- A square has four sides, four interior angles, and four vertices.
- All sides of a square are equal. (The sides AB, BC, DC and AD are all equal.)
- Each interior angle of a square equals $90^{\circ}$.
- The opposite sides of a square are parallel to each other.
- The diagonals of a square are equal.
- The diagonals of a square bisect each other at $90^{\circ}$.
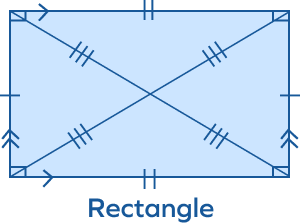
Properties of a Rectangle
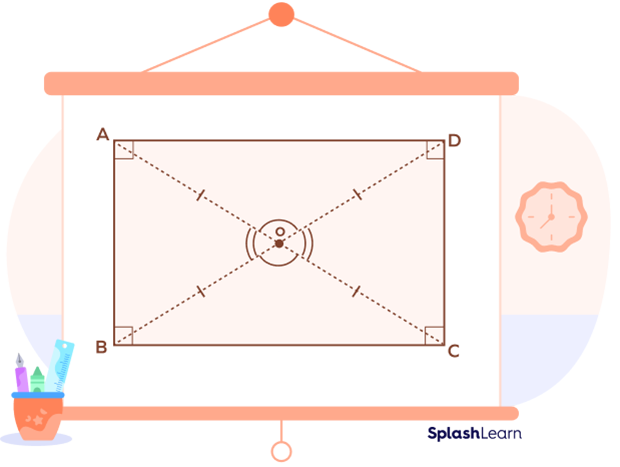
- A rectangle has four sides, four interior angles, and four vertices.
- The opposite sides of a rectangle are equal.
- Opposite sides of a rectangle are parallel to each other.
- All the interior angles in a rectangle measure $90^{\circ}$.
- The diagonals of a rectangle are equal.
- The diagonals of a rectangle bisect each other. They are not perpendicular. They form two angles, one acute and one obtuse.
Square vs. Rectangle
How are squares and rectangles alike? How do they differ from each other? Let’s compare and contrast squares and rectangles, and find out different similarities and differences.
| Square | Rectangle |
|---|---|
 |  |
| Squares are quadrilaterals. | Rectangles are quadrilaterals. |
| All four angles of a square are right angles. | All four angles of a rectangle are right angles. |
| Diagonals are equal in length. | Diagonals are equal in length. |
| Diagonals bisect each other. | Diagonals bisect each other. |
| Opposite sides are parallel. | Opposite sides are parallel. |
| Squares are a special type of parallelogram. | Rectangles are a special type of parallelogram. |
| Square is a regular polygon. | Rectangle is an irregular polygon. |
| All sides are equal. | Opposite sides are equal. |
| Diagonals are perpendicular. | Diagonals are not perpendicular. |
Difference between a Square and a Rectangle
Now, we have a good idea about squares and rectangles, their properties, and the basic differences. Let us summarize the difference between square and rectangle based on different properties like sides, diagonals, formulas for area and perimeter, etc.
| Property | Square | Rectangle |
|---|---|---|
| Sides | A square has four equal sides. Opposite sides are parallel. | A rectangle has four sides. Opposite sides are equal and parallel. |
| Diagonals | The diagonals of a square are equal. They bisect each other at $90^{\circ}$. Thus, diagonals are perpendicular bisectors. The length of the diagonal of a square $= \sqrt{2} \times side$ | The diagonals of a rectangle are equal. They bisect each other, but not at $90^{\circ}$. It means they are not perpendicular. The length of the diagonal of a rectangle $= \sqrt{length^{2} + width^{2}}$ |
| Area | The formula for the area of square $= side \times side$ | The formula for the area of a rectangle $= length \times breadth$ |
| Perimeter | The formula for the perimeter of a square $= 4 \times side$ | The formula for the perimeter of a rectangle $= 2 \times (length + width)$ |
Why Is a Square Also a Rectangle?
A square is considered a special kind of rectangle since it satisfies all the properties of a rectangle.
- They both have all interior angles of $90^{\circ}$.
- The opposite sides of both squares and rectangles are equal and parallel.
- The diagonals are equal. Also, diagonals bisect each other.
Thus, all squares are rectangles. However, all rectangles are not square since there are some properties of the square that do not apply to a rectangle.
- All sides of a square are equal.
- The diagonals of a square bisect each other at $90^{\circ}$.
Facts about Squares and Rectangles
Conclusion
In this article, we learned about differences and similarities between a square and a rectangle with the help of the definitions, table. Let’s solve a few examples and practice problems for better understanding.
Solved Examples on the Difference between Square and Rectangle
1. Find the area of the square with a side of 5 inches.
Solution:
Side $= 5$ inches
Area of square $= side \times side$
Area $= 5 \times 5$
$= 25\; inches^{2}$
2. Find the area and perimeter of a rectangle with length 8 inches and width 6 inches.
Solution:
Length $= 8$ inches
Width $= 6$ inches
Area of rectangle $= length \times width$
Area $= 8 \times 6 = 48\; inches^{2}$
Perimeter of rectangle $= 2 \times (length + width)$
$= 2 \times (8 + 6)$
$= 2 \times 14$
$= 28$ inches
Therefore, the area of the rectangle is $48\; inches^{2}$, and the perimeter of the rectangle is 28 inches.
3. The length of a rectangular field is 10 feet, and the width is 8 feet.
(i) What is the area of the field?
(ii) What will be the total length of the boundary of the given field?
Solution:
Length $= 10$ feet
Width $= 8$ feet
(i) To calculate the cost of painting the field, we need to find the area covered by the field.
Area of rectangle $= length \times width$
Area of field $= 10 \times 8$
$= 80\; feet^{2}$
(ii) Total length of the boundary $=$Perimeter of the field
Perimeter of rectangle $= 2 \times (length + width)$
Perimeter of the field $= 2 \times (10 + 8)$
$= 2 \times 18$
$= 36$ ft
4. Find the total area.
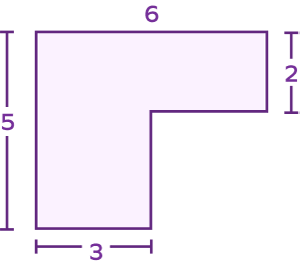
Solution:
The given figure is formed by a square and a rectangle.
We can divide it into a square having side 3 units and a rectangle of dimension 6 units 2 units.
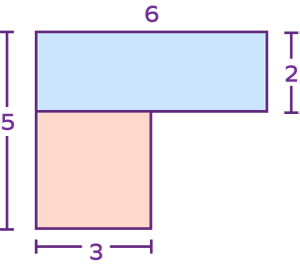
Area of the square $= side \times side = 3 \times 3 = 9$ square units
Area of the rectangle $= length\times breadth = 2 \times 6 = 12$ square units
Total area $= 9 + 12 = 21$ square units
Practice Problems on Difference between Square and Rectangle
Difference between Square and Rectangle - Definition, Examples, FAQs
The side of a square is z units in length. What will be the perimeter of the square?
The formula for the perimeter of a square is 4 side. Also, the perimeter is the sum of all sides.
Therefore, 4z units $= (z + z + z + z)$ units is the perimeter.
What is the area and perimeter of the given rectangle?

Area of rectangle $= length \times width = 11 \times 7 = 77\; \text{inches}^{2}$
Perimeter of rectangle $= 2 \times (length + width) = 2 \times (11 + 7) = 36$ inches.
Which of the following statements are not true about both squares and rectangles?
The diagonals of a square bisect at right angles. However, the diagonals of a rectangle only bisect each other. They are not perpendicular.
Frequently Asked Questions on the Difference between Square and Rectangle
Is a rectangle always a square?
No, a rectangle becomes a square when its length equals its breadth.
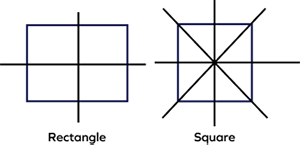
Do squares and rectangles have an equal number of lines of symmetry?
No, squares have 4 lines of symmetry, and they can be folded in half horizontally, vertically and diagonally, whereas rectangles have only 2 lines of symmetry; they can be folded in half horizontally and vertically.
Is a square a kite?
Yes, every square is a special form of a kite. A kite is a quadrilateral in which two pairs of sides are equal. The angles where two unequal sides meet are equal. A square satisfies all the conditions for being a kite.
Are rectangles and squares also parallelograms?
Yes! Opposite sides of a square and a rectangle are parallel and equal. Thus, they are parallelograms.
What does a square have in common with a rectangle?
All angles are right angles.
Opposite sides are equal and parallel.
Diagonals are equal and bisect each other.
Are diagonals equal in square and rectangle?
Yes. The diagonals of a square and a rectangle are of equal length.




































