What Is a Cuboid?
A cuboid is a three-dimensional shape having length, width and height. A cuboid is also called a rectangular prism.
Observe the shape of the fish tank shown here. What is its shape? Can you identify? This is a three-dimensional shape bounded by six rectangular faces. It is called cuboid.
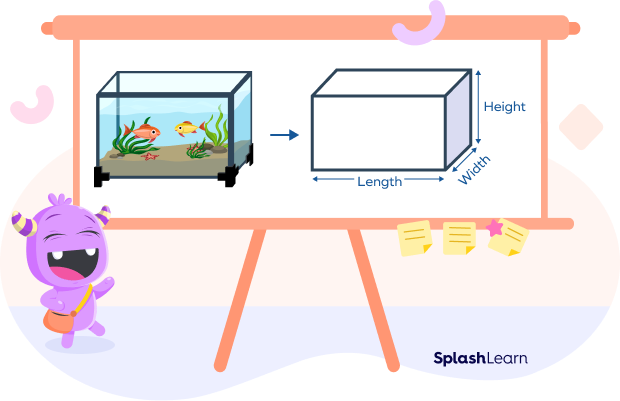
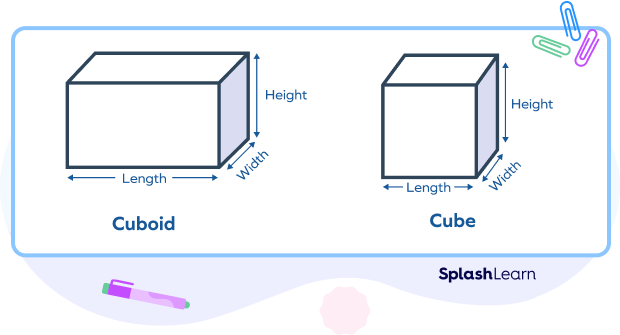
A cube is a special type of cuboid where the length, width and height are all equal.
Cuboid Shape
A cuboid shape is a 3D geometric solid whose each face is a rectangle. The cuboid shape is shown below.
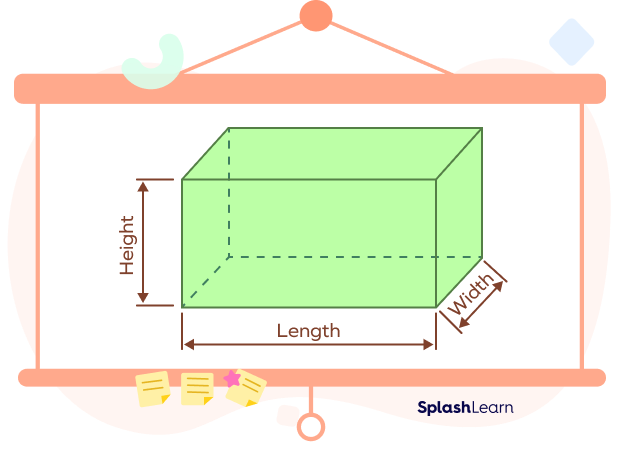
Dimensions of a Cuboid
The cuboid shape is determined by its 3 dimensions. Dimensions of a cuboid include its length, height, and width as shown in the figure.
Faces, Edges, and Vertices of a Cuboid
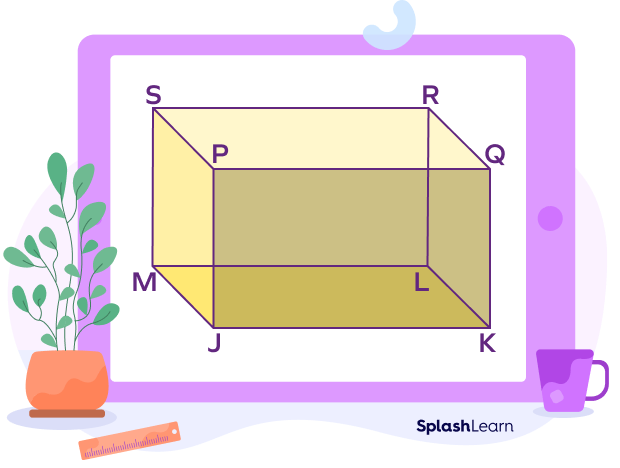
Every geometric solid has a finite number of faces, edges, and vertices. Vertices refer to the corner points. The vertices are joined by the edges. The flat surface bounded by the edges is called the face of a solid. Cuboid has 6 faces, 12 edges, and 8 vertices.
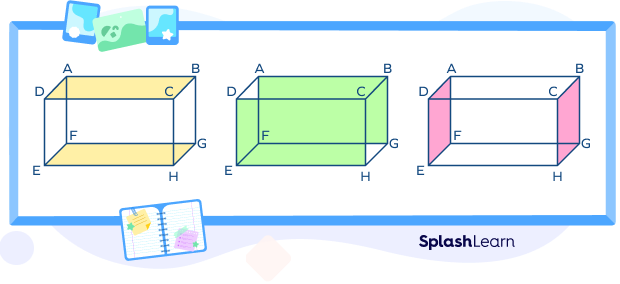
- Faces of a cuboid
Cuboid has 6 faces: 4 lateral, 2 identical faces at the top and bottom. All faces are rectangular in shape. Opposite faces are parallel.
Here, the faces are: ABCD, EFGH, ADEF, BCHG, ABFG and DCHE
The identical faces are ABCD and EFGH; ABFG and DCHE ; ADEF and BCHG.
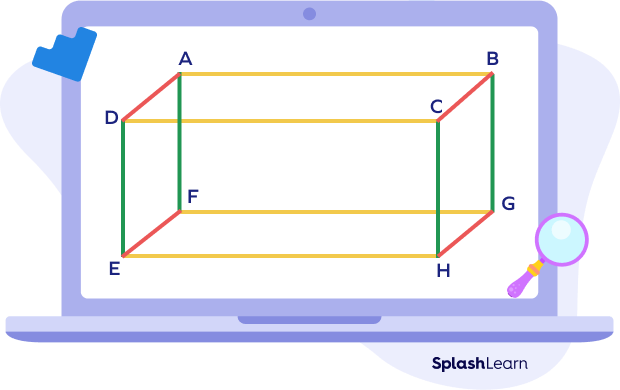
- Edges of a cube
A cuboid has 12 edges. The line segments AB, BC, CD, DA, DE, EF, FG, GH, EH, AF, BG and CH are edges of the given cuboid.
In cuboid, opposite edges are equal and parallel to each other.
Here,
AB = CD = EH = FG
AD = EF = GH = CD
And DE = AF = BG = CH
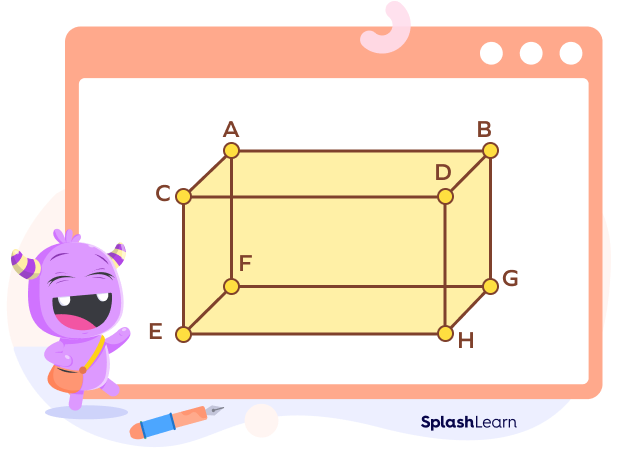
- Vertices of a cuboid
A cuboid has 8 vertices.
Here, the corner points A, B, C, D, E, F, G and H are the vertices of the given cuboid.
Properties of a Cuboid
- Vertices, Faces, Edges: A cuboid has 6 faces, 8 vertices, and 12 edges.
- A cuboid is a three-dimensional shape; it has length, width, and height.
- All the faces of a cuboid are rectangular in shape.
- All the angles that are formed at the vertices are right angles.
- All the opposite edges of a cuboid are parallel and equal to each other.
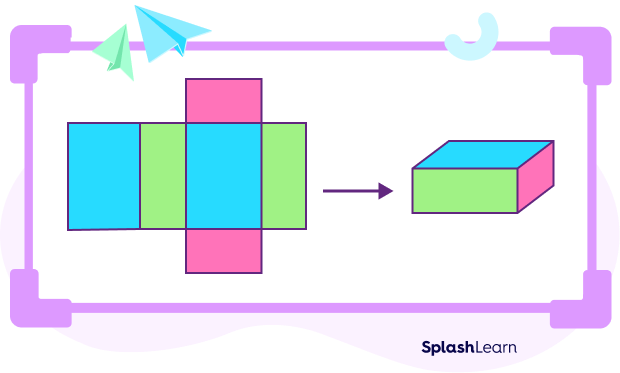
Net of a Cuboid
Net of a three-dimensional shape is the 2 dimensional shape we get when we unfold the solid and lay flat. Nets can be folded up to again make the 3D shapes.
Here, the view of the cuboid shape helps in identifying the sides that are rectangular in shape. Once the flattened shape is folded back together, the shape of a cuboid is formed.
Surface Area of Cuboid
The surface area of a cuboid can be divided into two types.
- Lateral surface area(LSA) of cuboid
Let l, w, and h be the length, breadth and height of a cuboid respectively.
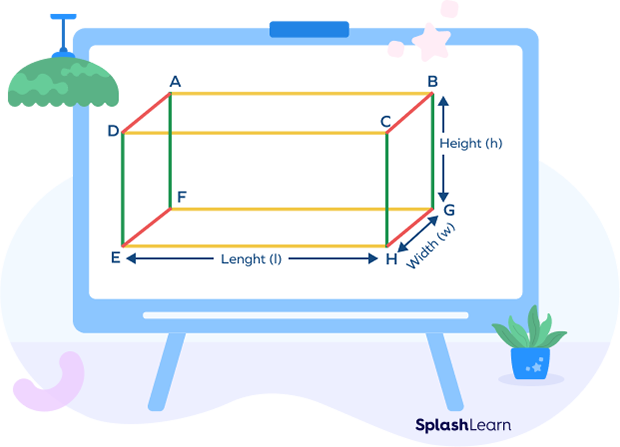
Lateral surface area (LSA) of a cuboid is the sum of areas of its four lateral faces except the top and bottom faces.
The unit of cuboid Lateral surface area (LSA) is measured in square units.
The lateral surface area of the cuboid = Area of face DEHC + Area of face CHGB + Area of face ABGF + Area of face DAFE
LSA of cuboid = (l × h) + (w × h) + (l × h) + (w × h) square units
LSA of cuboid = 2(l × h) + 2(w × h) square units
LSA of cuboid = 2h(l + w) square units.
- Total surface area of a cuboid:
Total surface area (TSA) of a cuboid = Sum of the areas of all its 6 rectangular faces.
TSA of cuboid = Area of face (ABCD + CDEH + CHGB + ABGF + DAFE)
TSA of cuboid = (l × w) + (l × w) + (w × h) + (w × h) + (l × h) + (l × h) square units
TSA of cuboid = (2lw + 2wh + 2lh) square units
TSA of cuboid = 2(lw + wh + lh) square units
Volume of a Cuboid
The volume of a cuboid is the space occupied by a cuboid. The volume of the cuboid is equal to the product of the base area (area of the rectangular face) and height. The volume is measured in cubic units.
Therefore, the formula to calculate the volume of a cuboid is:
Volume = (Length × width) × Height
= (l × w) × h
= lwh
Diagonals of a Cuboid
There are two types of diagonals in a cuboid:
- Face Diagonals
- Space Diagonals
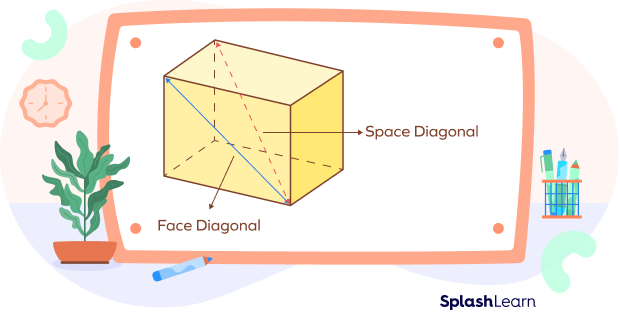
Generally In cuboid, we deal with space diagonal only. For each face there are two face diagonals. The total face diagonals in a cuboid are 6 faces $\times 2 = 12$.
- Formula for space diagonal of cuboid
Diagonal of cuboid whose length is l, width is w and height is h:
Length of space diagonal $= sqrt{l^{2} + w^{2} + h^{2}}$ units
Perimeter of a Cuboid
The perimeter of a cuboid is the sum of the lengths of all the edges.
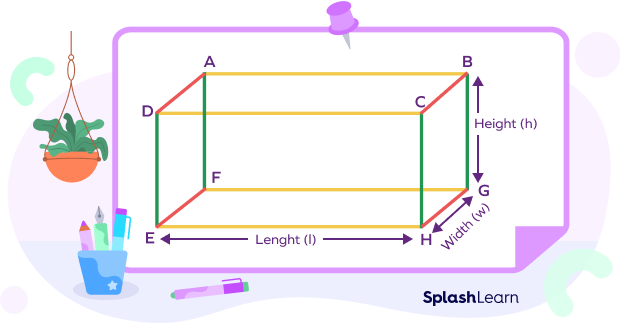
From the given figure, we have
- AB = CD = EH = FG = l (length)
- BC = AD = EF = HG = w (width)
- BG = CH = DE = AF = h (height)
Perimeter of a cuboid = AB + CD + EH + FG + BC + AD + EF + HG + BG + CH + DE + AF
= (l + l + l + l) + (w + w + w + w) + (h + h + h + h) units
= (4l + 4w + 4h) units
= 4(l + w + h) units
Cuboid Formulas Chart
The table below shows the formulas of a cuboid of length (l), width (w) and height (h).
| Measurement | Formula |
|---|---|
| Lateral Surface Area (LSA) | 2h(l + w) |
| Total Surface Area (TSA) | 2(lw + wh + hl) |
| Volume | lwh |
| Space Diagonal | $\sqrt{l^{2} + w^{2} + h^{2}}$ |
| Perimeter | 4(l + w + h) |
Cuboid Shaped Objects Around Us
There are many examples of cuboid you can identify in daily life. Take a look at various objects around us that have a cuboid shape!
Facts about Cuboid
- In geometry, a cuboid is a polyhedron. It is a hexahedron, a six-faced solid.
- A cuboid contains only right angles at their corner points. If there is any other type of angle, then it is not a cuboid.
- A cuboid is also a prism since it has a rectangular cross-section all the way through. It’s known as a rectangular prism.
- Every cube is also a cuboid, but every cuboid is not a cube.
- By the Euler’s formula the numbers of faces F, of vertices V, and of edges E of any convex polyhedron are related by the formula F + V = E + 2. In the case of a cuboid, this gives 6 + 8 = 12 + 2.
- Euler brick is a rectangular cuboid whose edges and face diagonals have integer lengths. A perfect cuboid is an Euler brick whose space diagonal also has an integer length.
Conclusion
In this article we learnt that a cuboid is a solid three-dimensional shape having length, width and height. It has 6 faces, 12 edges and 8 vertices. Each of its faces is a rectangle. It is also called a rectangular prism.
Solved Examples on Cuboid
Example 1: Calculate the lateral surface area of a cuboid of dimensions 11 cm × 5 cm × 4 cm.
Solution: Given dimensions of a cuboid are: 11 cm × 5 cm × 4 cm.
Let length(l) = 11 cm, width (w) = 5 cm, height (h) = 4 cm
Lateral surface area (LSA) = 2h(l + w) square units
= 2 × 4 (11 + 4) cm 2
= (8 × 15) cm2
= 120 cm2
Example 2: Find the total surface area (TSA) of this cuboid.
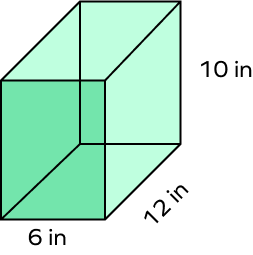
Solution:
Length (l) = 12 in, width (w) = 6 in, and height (h) = 10 in.
Total surface area of a cuboid = 2(lw + wh + lh) square units.
TSA = 2 {(12 × 6) + (6 × 10) + (12 × 10)} in²
TSA = 2 (72 + 60 + 120) in²
TSA = 2 (252)
TSA = 504 in²
Therefore, the required total surface area is 504 cm².
Example 3: Find out the volume of a rectangular prism with base length 9 inches, base width 6 inches, and height 18 inches, respectively.
Solution:
As we know the rectangular prism is a cuboid, we use the formula for the volume of the cuboid.
Length (l) = 9 inches
Width (w) = 6 inches
Height (h) = 18 inches
So, the volume of the given rectangular prism = l × w × h = 9 × 6 × 18 = 972 cubic inches.
Example 4: Find the length of the diagonal of a cuboid whose dimensions are 4 × 4 × 3 units.
Solution:
The length of the diagonal of a cuboid formula $= \sqrt{l^{2} + w^{2} + h^{2}}$ units.
Given length (l) = 4 units, width (w) = 4 units and height (h) = 3 units.
Therefore, the length of diagonal $= \sqrt{4^{2} + 4^{2} + 3^{2}}$ units
$= \sqrt{16 + 16 + 9}$ units
$= \sqrt{41}$ units
Therefore, the length of the diagonal is $\sqrt{41}$ units.
Example 5: Find the perimeter of a cuboid whose dimensions are 7 m × 4 m × 5 m.
Solution:
Length (l) = 7 m, width (w) = 4 m, and height (h) = 5 m
Perimeter of cuboid = 4 (l + w + h)
Perimeter of cuboid = 4 (7 + 4 + 5) m
P = (4 × 16) m
P = 64 m.
Practice Problems on Cuboid
Cuboid - Definition, Shape, Formulas, Properties, Examples, FAQs
What is the lateral surface area of a cuboid whose Length $= 3 \;cm$, Width $= 2 \;cm$ and Height $= 1 \;cm$?
As, lateral surface area (LSA) $= 2 \times h(l + w)$ sq.unit
So, lateral surface area of the given cuboid $= 2 \times 1(3 + 2) cm^{\circ} = 10\; cm^{\circ}$.
What is the total surface area of a cuboid whose Length $= 2\; cm$, Width $= 2\; cm$ and Height $= 2\; cm$?
Explanation: As, total surface area (TSA) $= 2 (l \times w + w \times h + l \times h)$ sq.unit
So, total surface area(TSA) of the given cuboid $= 2(2 \times 2 + 2 \times 2 + 2 \times 2 )\; cm^{2}$
$= 2 \times 12 cm^{2}$.
$= 24 \;cm^{2}$.
Sarah has a cuboidal box of dimensions $12 \times 7 \times 5$ inches. What is the volume of the box?
Volume of cuboidal box $= (12 \times 7 \times 5)$ cubic units
$= 420$ cubic units.
What is the perimeter of a cuboid whose Length $= 4\; cm$, Width $= 11\; cm$ and Height $= 2\; cm$?
Perimeter of cuboid $= 4 (l + w + h)$ units
So, perimeter of cuboid $= 4 (4 + 11 + 2)$ cm
$= (4 \times 17)$ cm
$= 68$ cm
Find the length of the diagonal of a cuboid whose dimensions are $10 \times 2 \times 4$ units.
Diagonal of a cuboid $= \sqrt{l^{2} + w^{2} + h^{2}}$ units.
Let $(l) = 10$ units, $(w) = 2$ units and $(h) = 4$ units.
Therefore, the length of diagonal $= \sqrt{10^{2} + 2^{2} + 4^{2}}$ units
$= \sqrt{100 + 4 + 16}$ units
$= \sqrt{120}$ units
Frequently Asked Questions about Cuboid
How can we define a cuboid?
A cuboid is defined as a three-dimensional shape that has six rectangular faces, eight vertices and twelve edges.
What is the main difference between a cuboid and a cube?
The main difference between a cube and cuboid is that a cube has all square faces and a cuboid has rectangular faces.
What is the difference between a rectangle and a cuboid?
The key difference is that a rectangle is a two-dimensional shape whereas a cuboid is a three-dimensional shape. Hence, a cuboid has an extra dimension, which is its height.
















