What Is the Difference between Area and Volume?
Area and volume of shapes are two fundamental measurements in geometry. Area is the measure of the space covered by a flat 2D surface, like the floor of a room. Volume, on the other hand, is the measure of the space occupied by a three-dimensional object, like a box.
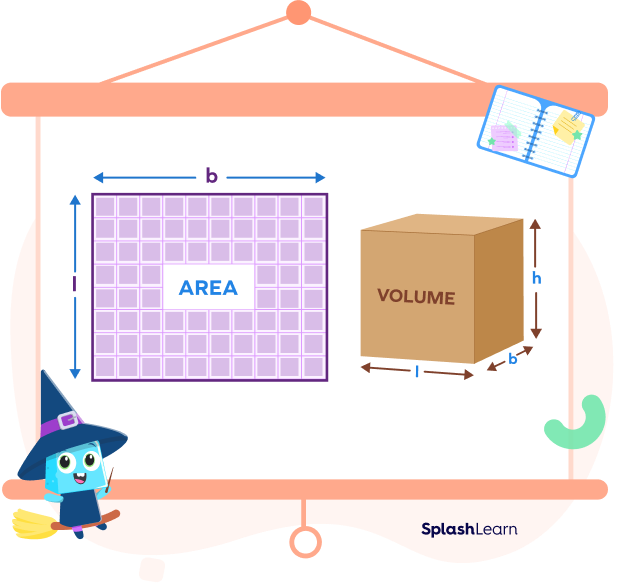
While area is expressed in square units (like square inches), volume is expressed in cubic units (like cubic inches). In simple terms, area deals with the surface space, while volume deals with the space inside an object.
Recommended Games
What Is Area?
Area is defined as the total space taken up by a flat (2D) surface or shape of an object.
Definition of Area in Geometry: The space enclosed by the boundary of a plane figure is known as its area. The area of a figure is the number of unit squares that perfectly cover the surface of a closed figure.
Area is measured in square units like square inches, square yards, etc. Area of a shape is a two dimensional quantity.
If you want to paint a rectangular wall of your house, you need to know the Area of the wall to calculate the quantity of the paint required to paint the wall and the cost of painting.
Recommended Worksheets
What Is Volume?
Every three-dimensional object occupies some space. This space is measured in terms of its volume.
Definition of Volume in Geometry: Volume is defined as the space occupied within the boundaries of an object in three-dimensional space.
Volume refers to the three-dimensional space inside an object, while capacity specifically refers to the amount a container can hold.
When building a fish tank, understanding the Volume of the tank helps determine how much water it can hold and what size of a filter or pump is needed.
Difference Between Area and Volume
| Area | Volume |
|---|---|
| It is defined for two dimensional shapes. | It is defined for three dimensional objects. |
| Area refers to the space taken up by a flat, two-dimensional shape on a surface. | Volume pertains to the amount of space occupied by a three-dimensional object. |
| It is expressed in square units like square inches, square feet, etc. | It is expressed in cubic units like cubic inches, cubic feet, etc. |
| Examples of 2D shapes: quadrilaterals, circles, polygons, etc. | Examples of 3D shapes: cube, cuboid, sphere, etc. |
Formulas for Area and Volume
The area and volume formulas for different two-dimensional and three-dimensional shapes are listed in the tables given below. Calculating area and volume becomes easier once you know the required dimensions. Just substitute the values in the formula and assign the appropriate unit.
Area Formula Chart for 2D shapes
| Geometric shapes | Dimensions | Area formula |
|---|---|---|
| Square | a = side of square | A $= a^{2}$ |
| Rectangle | l = length, w = width | A $= l \times w$ |
| Triangle | b = base, h = height | A $= \frac{1}{2} \times b \times h$ |
| Parallelogram | b = base, h = height | A $= b \times h$ |
| Rhombus | a = side of rhombus, h = height | A $= a \times h$ |
| Circle | r = radius of circle | A $= \pi r^{2}$ |
| Semicircle | r = radius of semicircle | A $= \frac{1}{2} \pi r^{2}$ |
| Trapezoid | a and b = bases, h = height | A $= \frac{1}{2} \times (a + b) \times h$ |
Volume Formula Chart for 2D shapes
| Geometric shapes | Dimensions | Volume formula |
|---|---|---|
| Cube | a = side of square | V $= a^{3}$ |
| Cuboid | l = length, w = width, h = height | V $= l \times w \times h$ |
| Right Circular Cone | r = radius of circular base, h = height of cone | V $= \frac{1}{3} \pi r^{2}h$ |
| Right Circular Cylinder | r = radius of circular base, h = height of cylinder | V $= \pi r^{2}h$ |
| Sphere | r = radius of sphere | V $= \frac{4}{3} \pi r^{3}$ |
| Hemisphere | r = radius of hemisphere | V $= \frac{2}{3} \pi r^{3}$ |
| Right Pyramid | V $= \frac{1}{3} \times$ (Area of base) $\times$ height | |
| Right Prism | V = Area of base $\times$ height | |
Facts about Difference between Area and Volume
- Area pertains to two-dimensional space within a flat shape.
- Volume involves the capacity occupied by a three-dimensional object.
- Area is measured in square units (e.g., square inches, square meters).
- Volume is measured in cubic units (e.g., cubic centimeters, cubic feet).
- Area is used for measuring surfaces like walls, floors, and 2D shapes.
- Volume is used for measuring capacity, such as the contents of a container or 3D objects.
Conclusion
In this article, we explored the distinction between area and volume, understanding that area refers to the space within a flat shape while volume encompasses the capacity of a three-dimensional object. Let’s check our understanding by attempting practice exercises and solving examples.
Solved Examples on Difference between Area and Volume
1. The dimensions of a rectangle are 12 inches and 9 inches. Find its area.
Solution:
Length = 12 inches
Breadth = 9 inches
Area = Length $\times$ Breadth
Area = 12 $\times$ 9
Area = 108 square inches
2. What is the volume of the cone whose base radius is 7 feet and height is 12 feet?
Solution:
Base Radius (r) = 7 feet
Height (h) = 10 feet
Volume of the cone $= \frac{1}{3} \pi r^{2}h$
Volume of the cone $= \frac{1}{3} \times \frac{22}{7} \times 7 \times 7 \times 12$
Volume of the cone = 616 cubic feet
3. Find the area of a triangle with base 3 feet and height 6 feet.
Solution:
Base (b) = 3 feet
Height (h) = 6 feet
Area $= \frac{1}{2} \times b \times h$
Area $= \frac{1}{2} \times 3 \times 6 = 9$ square feet
4. The radius of a sphere is 10.5 inches. Find the volume of the sphere.
Solution:
Radius (r) = 10.5 inches
Volume of the sphere $= \frac{4}{3} \pi r^{3}$
Volume of the sphere $= \frac{4}{3} \times \frac{22}{7} \times 10.5 \times 10.5 \times 10.5$
Volume of the sphere = 4851 cubic feet
5. A square with side 2 inches is cut out from a corner of a larger square sheet of side 6 inches. Find the area of the remaining square sheet.
Solution:
Side of large square = 6 inches
Area of the large square $= 6 \times 6 = 36$ square inches
Side of small square = 2 inches
Area of the small square $= 2 \times 2 = 4$ square inches
Area of the remaining sheet = Area of the large square – Area of the small square
Area of the remaining sheet = 36 – 4 = 32 square inches
Practice Problems on Difference between Area and Volume
Difference Between Area and Volume - Definition, Formulas, FAQs
What is area?
Area is the amount of space occupied by a two-dimensional shape.
What does volume measure?
Volume measures the space occupied by a three-dimensional object.
Which of the following objects have a volume?
A can of tune is a 3D object (usually comes in cylindrical shape). It has volume. All the other options are 2D shapes.
Area of rectangle =
Area of the rectangle $= Length \times Breadth$
If area of base of a right pyramid is 9 square feet and height is 15 square feet, the volume will be :
Area of base (A) = 9 square feet
Height (h) = 15 square feet
V $= \frac{1}{3} \times$ (Area of base) $\times$ height
V $= \frac{1}{3} \times 9 \times 15 = 45$ cubic feet
Frequently Asked Questions on Difference between Area and Volume
What is the difference between Perimeter and Area?
Perimeter is the length of the boundary of a two dimensional shape whereas Area is the space occupied by a two dimensional shape or object.
What is the Surface Area?
The area occupied by a three-dimensional object by its outer surface is called the surface area.
What is the difference between Area and Surface Area?
Area is the space occupied by a two dimensional object whereas surface area is the total area of the outer surfaces of an object.
What’s the difference between area and volume?
Area is the space inside a 2D shape, while volume is the space occupied by a 3D object.




































