Positive Rational Numbers – Definition, Reciprocal, Examples, FAQs

What Are Positive Rational Numbers?

A positive rational number is a rational number in which both numerator and denominator have the same sign.

In other words, positive rational numbers are rational numbers in which both the numerator and the denominator can be either positive integers or negative integers.

Positive rational numbers examples: $\frac{3}{7},\;\frac{4}{5},\;\frac{-\;12}{-\;19}$, etc.

What Are Rational Numbers?

Rational numbers are numbers that can be written in the form pq, where p and q are integers and q ≠ 0.

Thus, the rational numbers not only include all the integers Z = {…, -3, -2,-1,0,1,2,3,…}, but also all the fractions or the numbers between any two integers which can be written in the rational form$\frac{p}{q}$, where p and q are integers and q ≠ 0.

Note: The difference between rational numbers and fractions lies in the fact that fractions cannot have negative numerator or denominator. Hence, the numerator and denominator of a fraction are whole numbers (denominator ≠ 0), whereas in the case of rational numbers, the numerator and denominator are integers. Rational numbers can be positive, negative and 0.

Positive Rational Numbers: Definition

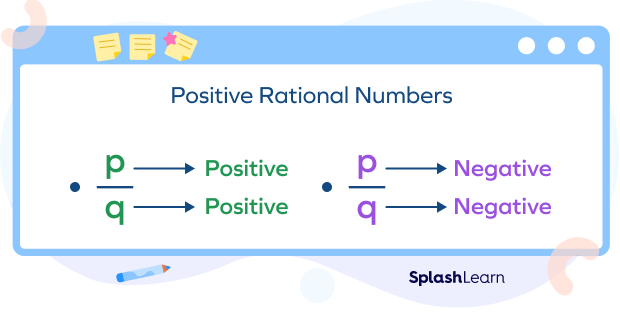
Positive rational numbers are the rational number of the form $\frac{p}{q}$, where p and q are integers having the same sign (both positive or both negative) and q ≠ 0.

Case 1: When both p and q are positive integers

Here, both numerator and denominator are positive integers. Thus, the resulting rational number is also positive.

Example: $\frac{6}{7},\;\frac{18}{25}$

Case 2: When both p and q are negative integers

Here, both numerator and denominator are negative integers. If you multiply both numerator and denominator by -1, we will get an equivalent rational number in which both numerator and denominator are positive. Thus, when both numerator and denominator are negative integers, the rational number is a positive rational number.

Example: $\frac{-\;6}{-\;7} = \frac{6}{7},\;\frac{-\;18}{-\;25} = \frac{18}{25}$

Properties of Positive Rational Numbers

• Positive rational numbers are always greater than zero and are positioned to the right of zero on the number line.
• They can be expressed as a fraction with a positive numerator and denominator.
• Positive rational numbers are closed under addition and multiplication.
• The sum of two positive rational numbers is always a positive rational number.
• The product of two positive rational numbers is always a positive rational number.
• Positive rational numbers can be written as terminating decimals or recurring decimals.

Is 0 a Positive Rational Number?

0 is neither a positive nor a negative rational number. Rational numbers are classified as positive, zero, or negative rational numbers.

Thus, 0 is not a positive rational number.

Is Every Natural Number a Positive Rational Number?

Every natural number is a positive rational number since a natural number “n” can be written as $n = \frac{n}{1}$, where both n and 1 are positive integers.

Examples: $9 = \frac{9}{1}, 1 = \frac{1}{1}$

Positive Rational Numbers Less Than 1

0 is not a rational number.

1 is a positive rational number.

There are infinitely many rational numbers between any two rational numbers.

Here are a few positive rational numbers between 0 and 1:

• $\frac{1}{2} = 0.5$
• $\frac{1}{3} = 0.33$…
• $\frac{1}{4} = 0.25$
• $\frac{1}{5} = 0.2$
• $\frac{3}{5} = 0.6$

Positive Rational Numbers vs. Negative Rational Numbers

Positive Rational Numbers	Negative Rational Numbers
In a positive rational number, both numerator and denominator have the same signs	In a negative rational number, both numerator and denominator have opposite signs
Examples: $\frac{3}{4},\;\frac{-\;5}{-\;6},\;\frac{21}{29}$	Examples: $\frac{3}{-\;4},\;\frac{-\;5}{6},\;\frac{-\;21}{29}$
Positive rational numbers are greater than 0.	Negative rational numbers are less than 0.
They are located to the right of 0 on the number line.	They are located to the left of 0 on the number line.

Positive Rational Numbers: Symbol

The set of rational numbers can be denoted by the symbol Q. 

Positive Rational Numbers can be denoted by the symbol Q+. 

Reciprocal of a Positive Rational Number

The reciprocal of a positive rational number is also a positive rational number.

The reciprocal of a positive rational number can be obtained by interchanging the values of the numerator and the denominator.

Reciprocal of $\frac{a}{b}(b\neq 0)$ is $\frac{b}{a}$.

The product of the positive rational number and its reciprocal is always 1.

Example: Reciprocal of $\frac{3}{4}$ is $\frac{4}{3}$. 

Facts about Positive Rational Numbers

Solved Examples on Positive Rational Numbers

1. Are all whole numbers positive rational numbers?

Solution: 

Whole numbers = {0, 1, 2, 3, 4, …}

0 is not a positive rational number.

Thus, all whole numbers are not positive rational numbers. Whole numbers except 0 (which are called natural numbers) are positive rational numbers.

2. Is $\frac{-\;22}{-\;25}$ a positive or negative rational number?

Solution: 

$\frac{-\;22}{-\;25}$ is a positive rational number as both numerator and denominator have negative signs. 

If we multiply and divide both numerator and denominator by -1, we get 

$\frac{-\;22 \times (-\;1)}{-\;25 \times (-\;1)} = \frac{22}{25}$

Thus, $\frac{-22}{-\;25}$ is a positive rational number.

3. Find the reciprocal of $\frac{18}{25}$.

Solution:

Reciprocal of $\frac{a}{b} (b \neq 0)$ is $\frac{b}{a}$.

Reciprocal of $\frac{18}{25} = \frac{1}{\frac{18}{25}} = \frac{25}{18}$

Practice Problems on Positive Rational Numbers

Frequently Asked Questions about Positive Rational Numbers